The Self-Made Tapestry

Philip Ball (1999)

CONTENTS
1. PATTERNS
2. BUBBLES
3. WAVES
4. BODIES
5. BRANCHES
6. BREAKDOWNS
7. FLUIDS
8. GRAINS
9. COMMUNITIES
10. PRINCIPLES

If there is one thing I hope to do in this book, it is to shake up these assumptions. I wish to show in particular that pattern and organized complexity of form need not arise from something as complicated as life, but can be created by simple physical laws. This idea of complexity from simplicity has become almost a new scientific paradigm in recent years, and most probably a cliche too. Yet I hope here to tie it down, to show that it is not a recondite solution to all of life's mysteries, nor a result of a newly acquired facility for tricky computer modelling, nor even a particularly new discovery—but a theme that has featured in scientific enquiry for centuries. Some of the complex patterns that I shall consider in this book pose questions that are truly ancient: from where come the stripes of a tiger, the procession of 'mare's tail' clouds, the undulations of sand dunes, the vortex of a whirlpool, the shapes and decorative adornments of sea shells? (2)

The objection that it would take an unreasonably long time to find the best form from the range of alternatives—a favourite argument for evolutionary sceptics—crumbles beneath the extraordinary and demonstrable efficiency of natural selection. We can watch the process take place in a matter of days for generations of bacteria bred in culture. In 1994, Swedish researchers performed computer experiments showing that even a biological device as sophisticated as an eye will evolve from a flat sandwich of photosensitive cells in a matter of around 400,000 generations—perhaps half-a-million years, a blink in geological terms-if one makes conservative assumptions about such factors as the rate of mutation between each generation. Even getting life started in the first place, from a brew of simple organic chemicals on the young Earth, seems to have been astonishingly easy: it may have taken less than 200 million years from the time that the planet first had a solid surface, and would presumably have involved competition and consequent selection amongst generations of replicating molecules and small molecular assemblies. (5-6)

Once you start to ask the 'how?' of mechanism, you are up against the rules of chemistry, physics and mechanics, and the question becomes not just 'is the form successful?' but 'is it physically possible?'
Questions of this sort were what prompted the Scottish zoologist D'Arcy Wentworth Thompson in 1917 to write a beautiful book whose influence is still felt today. In On Growth and Form, Thompson gave an engineer's answer to the Darwinism that was rushing like a deluge through the biology of his time. Still in its first flush, Darwin's theory was propounded as the answer to every question that someone in Thompson's community might want to ask. The shape of a goat's horn, of a jellyfish's protoplasmic body, of a sea shell—all have the form they do because natural selection has sculpted them that way.
D'Arcy Thompson saw such ideas as an affront to one of science's guiding principles: economy of hypotheses. (6)

What, suggested Thompson, could be more unnecessary than invoking millions of years of selective fine tuning to explain the shape of a horn or a shell when one could propose a very simple growth law, based on proximate physical causes, to account for it? The sabre-like sweep of an ibex horn does not have to be selected from a gallery of bizarre and ornate alternative horn shapes: one can merely assume that the horn grows at a progressively slower rate from one side of the circumference to the other, and hey presto—you have an arc. (7)

It's not unusual to associate pattern with order: creating a recognizable pattern rather than a mess requires an orderly process of putting the pieces in place. It is, then, possibly a little alarming to discover that in nature the most highly symmetrical systems are also the most random. (15)

Surface tension and surface excess energy are two equivalent manifestations of the fact that surfaces are less stable than the interior of a substance. This means that surfaces cost energy. As all physical systems like to reach their most energetically stable state (that is, their equilibrium state), they tend to minimize the area of their surfaces. (18)

Everyone knows that, while it is well-nigh impossible to blow bubbles from pure water, they can be made in abundance from water to which a little soap or detergent has been added. Soaps contain molecules called surfactants, which have a tendency to migrate from the bulk of the liquid to the surface, where their presence greatly reduces the surface tension. This means that surfaces cost less, and a larger surface area can be sustained. Notice that, although our intuition tells us that bubbles have a 'stronger skin' than pure water, they can exist at all only because their surface tension is lower. (19)

Amongst the sprawling modern myth of Thomas Pynchon's Gravity's Rainbow is a fleeting reference to a man who tried to make patterned paint. The reference is clearly meant to document a quixotic, absurd ambition, for we all know that paint does not unmix into the separate pigments that went into its making.
But life is always stranger than we think. Take a look at Plate 4. Pynchon's ill-fated entrepreneur would have done well to follow the recipe that produced these blue and yellow stripes; for this is indeed a stable pattern that emerges spontaneously from a mixture of chemical compounds. (50)

To sustain indefinitely the oscillations of the BZ reaction, we also need a source of energy. In practice this supply can take the form of a constant throughflow of reactants and products: the reaction can be conducted in a stirred vessel in which fresh reactants are constantly supplied and end products withdrawn. Such vessels are called continuous stirred-tank reactors (CSTRs). Living organisms can be considered as approximations to CSTRs insofar as they (we) continually (though perhaps not continuously) ingest food (fresh material for metabolism) and excrete waste products. In this way we sustain our out-of-equilibrium (and sometimes oscillatory) biochemistry. (52)

Smolin argues that certain aspects of the star-formation process give it characteristics akin to a diffusion process. The galaxy then becomes an action-diffusion system, with all the pattern-forming potential that entails—making it permissible to view these cosmic pinwheels as gargantuan relatives of the whorls on a frog's egg.
Yes, say hello to life's universal patterns. We'll be seeing more of them. (76)

The patterns on animal tails may be either spots or bands, but bands always appear as the tail tapers towards the end. (86)

This topic shows how a little knowledge can simply make life harder. In the eighteenth century no one was troubled by the question of how babies grow from embryos, because it was assumed that, naturally enough, all creatures start life as miniature but fully formed versions of their adult selves, and just grow larger. People, it was thought, grow from microscopic homunculi in the womb, which possess arms, legs, eyes and fingers perfect in every detail. The problem with this idea, which was rather swept under the carpet, is it it entails an infinite regression: unless you are prepared to accept the formation of pattern from a shape's egg at some stage, you have to assume that the female homunculi contain even smaller homunculi in their tiny ovaries, and so on for all future generations. (99)

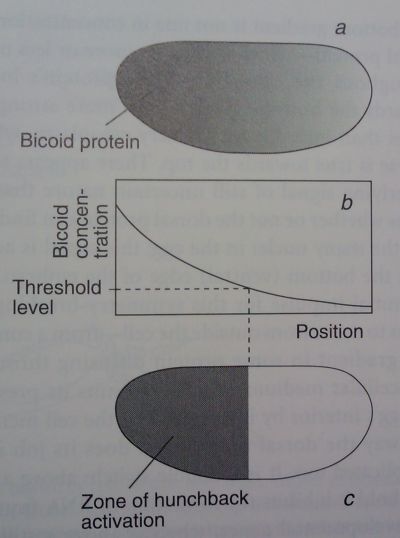
ZONE OF HUNCHBACK ACTIVATION:

It turns out that the phyllotaxis in any plant species correspond to pairs in [the Fibonacci] series. A corollary of this is that the number of petals on most flowers corresponds to a Fibonacci number: buttercups have five, marigolds have 13, asters 21. (106)

The situation is mathematically equivalent to the Saffman-Taylor instability in viscous fingering, with the pressure gradient in the latter case playing the same role as the temperature gradient here. If the Mullins-Sekerka instability alone acted on a rapidly advancing solidification front, an initially circular crystal might be expected to develop into a tenuous shape like a DLA cluster. But at the interface between a real solid and its melt there is again a surface tension, and it moderates the effect of the instability, just as it does for viscous fingering, by imposing a minimum size limit on the fingers. (124)

The relationship between metabolic rate and size is a long-standing puzzle. It is common knowledge that the rate of a creature's heartbeat decreases as its body size increases: babies' hearts beat faster than those of adults (they also breathe faster), and the heartbeats of small creatures like birds are more rapid still. For a wide variety of organisms, the heartbeat rate turns out to be proportional to the inverse of the body mass raised to power 1/4. The metabolic rate of individual cells in an organism—the rate at which they consume energy follows the same mathematical law. In other words, big organisms have a slower metabolism. (132)

One of the most common features of a great many crack patterns, however, is that they are fractal: the network of cracks defines a structure whose dimensionality is not a whole number. (146)

Mandelbrot realized in the 1970s that the natural topography of the Earth is typically a self-affine fractal. He notes how this aspect of mountain landscapes can be discerned in Edward Whymper's comments from Scrambles Amongst the Alps in 1860-1869: 'It is worthy of remark that ... fragments of ... rock ... often present the characteristic forms of the cliffs from which they have been broken'. Fractal geometry has since been used to produce stunning simulated images of imaginary mountainous terrain, and to manufacture computer-generated but realistic-seeming landscapes in Hollywood movies. The crucial point here is that these landscapes are not simply random; if you let the computer generate an image in which the ups and downs are merely determined by a random process, the result is a relief pattern that is certainly uneven but that just looks strange. Fractal landscapes are 'noisy' and unpredictable, but are not simply random. (160-1)

So you might, when next walking in the mountains, like to scan the slopes all around for miniature replicas of the giant peaks in the distance: demonstrations of the Earth's scale invariance carved by the elemental forces of nature. (164)

If you want to see one of the key differences between Eastern and Western thought, look at the classical art of the two cultures. The West is deeply concerned with static form, with the angle of hand and arm, the tilt of a head, the naturalistic reproduction of shape. The Eastern tradition works differently: not with light and shade, not with a limitless blend of mimetic colour, but with quick, broad strokes, alive with the energy of the artist. It is like the apotheosis of a sketcher's technique, capturing the instant while exclaiming the transience of forms in motion. It is, in short, an art that embraces change—an embodiment of the essential difference between a Platonic and a Taoist tradition.
Traditional Western artists have seldom faced up squarely to the challenge of change. It's not easy to paint something that is never still. Yet to the traditional Chinese artist, that can be the whole point of the exercise: capture the fundamental forms of motion. This is nowhere more clear than in the ways in which these two traditions have attempted to depict the most challenging of all movements: that of flowing water. The West has relied on the play of light to suggest the froth of wave caps (take a look at George Morland's The Wreckers (1791) or the swirl of mist and sea (take a look at almost any painting by Joseph Turner). Chinese and Japanese artists, meanwhile, have sought to capture the structures of fluid trajectories in a series of lines, which are remarkably close to the streamlines that scientists use to depict fluid flows (as we shall see).
This is not a naturalistic representation, but an artistic response to the same problem that now occupies a great many physical scientists: what are the fundamental forms of turbulent flow? (165)

If there's one thing that has become clear, it is that granular media are seldom predictable. Shaking together different kinds of grains can either ensure good mixing or have the opposite effect of causing them to congregate according to their size. Sound waves can bend through a right angle as they travel through sand, while the stress below a sand pile has a minimum where the pile is highest. The pressure at the bottom of a tall column of sand does not depend on its height, and this is why a sand glass is a good timekeeper—the sand leaks away at a steady rate even though the column gets smaller. If water were like this, the pressure at the sea would be no greater than that a few metres below the surface. (199)

One of the most striking outcomes of investigations into the fundamental nature of grainy materials is the realization that they represent rich ground for the appearance of patterns and form. Some of these patterns show many of the same features as those seen in other, completely different, systems; granular media can provide a convenient model system for studying complex phenomena as diverse as the fluctuations of stock markets and the formation of large-scale structure in the Universe. (199-200)

Thus, shaking, tumbling or even simple pouring of granular media can cause a mixture of different grains to mix, unmix or form striking patterns. At present there is no general theory that allows us to predict which of these will take place for a given system: again, you don't know until you try it. (210)

But here is the curious thing: in their model, Bak and colleagues found that a single grain can induce a landslide of any magnitude. It might set only a few grains tumbling, or it might bring about a catastrophic sloughing of the entire pile. There is no way of telling which it will be. (210)

I don't think that we have by any means exhausted the capacity of granular substances to generate spontaneous patterns, nor have I been able here to survey all of those that are currently known. What is particularly exciting about these systems is that not even the scientists studying them have yet acquired the kind of intuition that allows them to predict what they might see in a given experiment. You have to shake it and see! And I feel there is an attraction too in a kind of physics that returns to the spirit of the nineteenth-century pioneers like Michael Faraday, performing simple bench-top experiments with cheap, homemade equipment and a mind that is prepared to be astonished at the artistry of nature. There is much we can learn from playing in the sand. . . . (222)